Prince Arora and Vivek Agarwal
Introduction
Mental Spaces
Mental spaces can be thought of as small conceptual packets which are constructed while we talk, think, interact and act. They can be modified during the course of the thought.
Generic Spaces
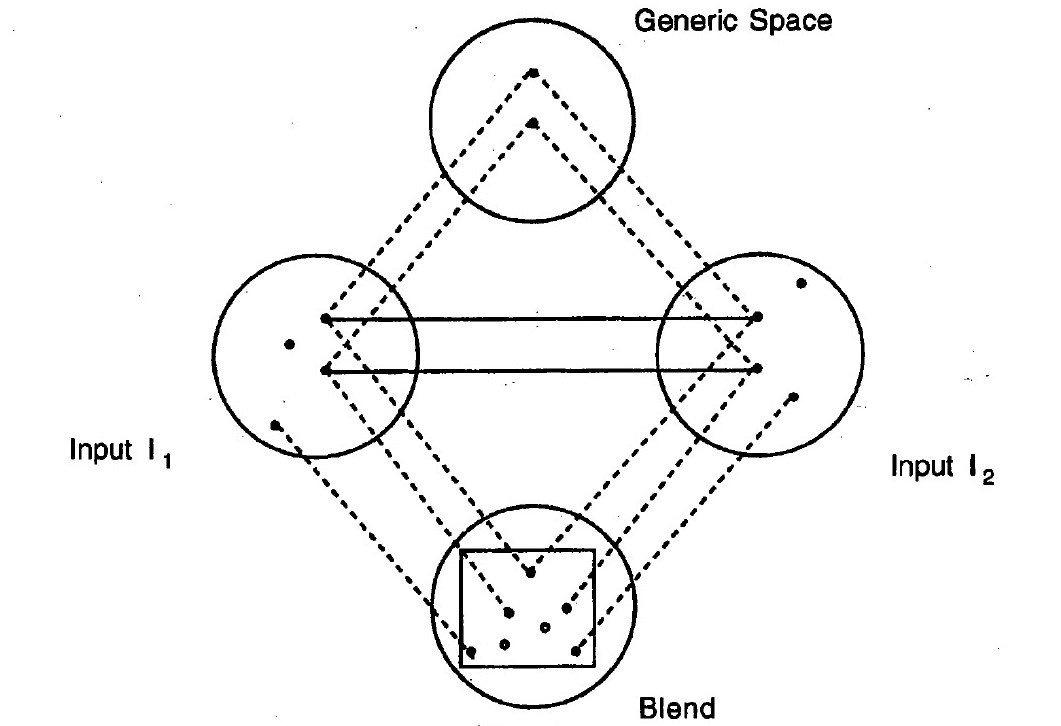
As input spaces are created, whatever structure belongs to both of the input spaces, constitutes a generic space. At any moment , the generic space maps onto each of the inputs. It defines the current cross-space mapping between them. A given element in the generic space maps onto paired counterparts in the two input spaces.
What is Cognitive Blending ?
Cognitive Blending is a Cognitive Process that operates over the mental spaces as inputs i.e. to say the structure from two input spaces is projected to a seperate space, "the blend". The blend itself has properties and structures of its own and also partly inherits them from the input spaces.
Analogy
Think of it as a chemical reaction where the final compound has properties of its own and sometimes properties of the reactacts also.
What does Cognitive Blending do?
Cognitive Blending provides one with a structure that presents all the interacting Mental Spaces in a way which is not available in any of the individual spaces and enormus efficiency.
Source: #1
Illustration
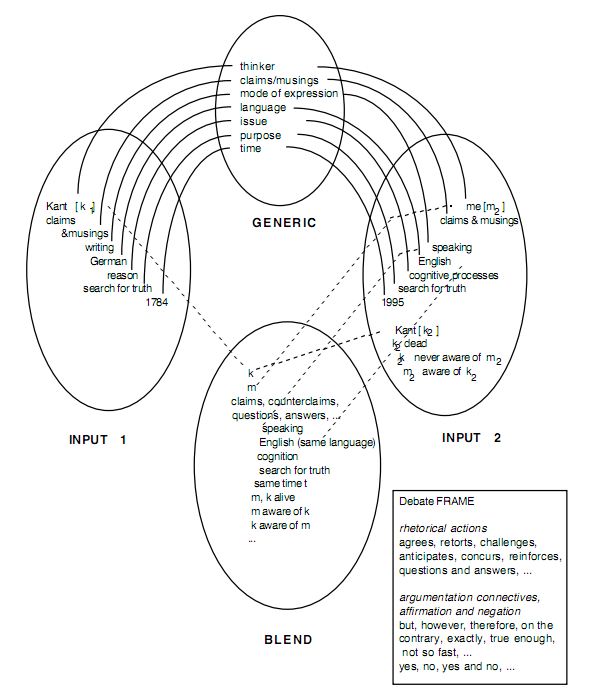
The Debate with Kant
Consider:
I claim that reason is a self-developing capacity. Kant disagrees with me on this point. He says it's innate,
but I answer that that's begging the question, to which he counters, in Critique of Pure Reason, that only
innate ideas have power. But I say to that, what about neuronal group selection? And he gives no answer.
In the first input space there is Modern Philosopher, making claims. In the second input space we have Kant, thinking and writing. Clearly, in neither of the spaces there is a Debate. Both of these mental spaces share common frame structure: a thinker, claims and musings, language, et cetera. This shared mental space forms the generic space. This give rise to the blend. This frame also additionally inherits the frame of debate; apperaing as Kant and the modern philospher are in a process of a continual debate.
Source: #2
Characteristics of Blending
Blending exploits and develops counterpart connections between inputs. Any two counterparts may or may not be fused in the blend.
Language and modes of expression are fused while the philosophers themseleves are not fused.
Blending has effects like; conceptual integration of related events into one complex event, evolution and use in the blend of frames not necessary for its inputs, and the development of novel conceptual structure.
Complex Event: Debate
Conceptual Structure: The time of the debate is a very unusual kind of time
Cognitive work like reasoning, drawing inference and developing emotions happends in the blended spaces.
Reasoning: Philosopher's Intellectual Inquiry; Inference: Kant beg the question put by the philosopher, and blamed for it.
In blending, conceptual work may be employed in the conceptual array. Spaces, domains and frames might proliferate and be modified. Blending can be applied successively during that proliferation.
Principles (Source #3)
Through selective projection, expressions applied to an input can be projected to apply to counterparts in
the blend. In this way, blends harness existing words in order to express the new meanings that arise in the
blend.
Combinations of expressions from the inputs may be appropriate for picking out structure in the blend even
though those combinations are inappropriate for the inputs. In consequence, grammatical but meaningless
phrases can become grammatical and meaningful for the blend.
Application
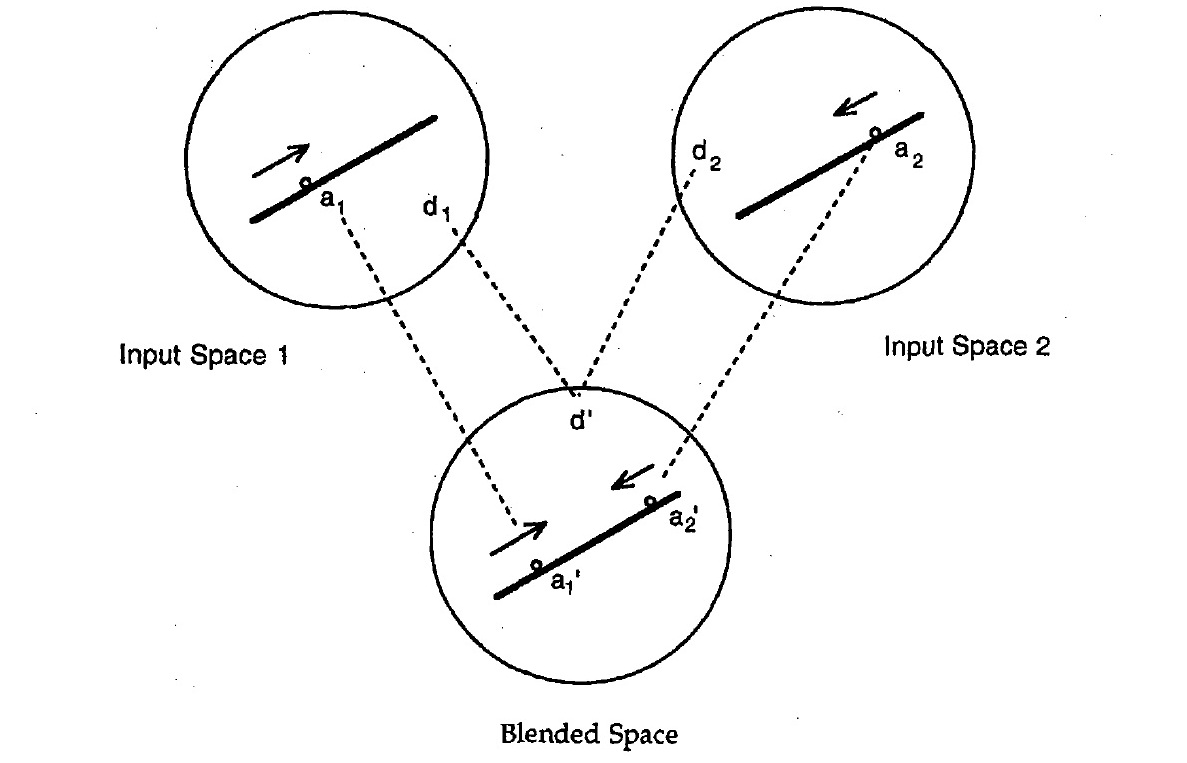
The Riddle of the Buddhist Monk
Consider a classic puzzle of inferential problem-solving (Koestler, 1964):
A Buddhist monk begins at dawn one day walking up a mountain, reaches the top at sunset, meditates at the top for several days until one dawn when he begins to walk back to the foot of the mountain, which he reaches at sunset, Making no assumptions about his starting or stopping or about his pace during the trips, prove that there is a place on the path which he occupies at the same hour of the day on the two separate journeys.
Source: #1
In this example, the monks, paths, journeys, days, and so on are counterparts.
The two input spaces have two journeys completely separated in time; the blend has two simultaneous journeys. Blends can contain structures that are impossible for the inputs, such as two monks who are the same monk.
Complex Numbers
INPUT SPACES
Euclidean Plane.
Real Numbers.
BLEND
Complex Number, is both a number and a point. One could say that the concept of representing real numbers on a line is extended to both dimensions. Clearly,using principle 1,a complex number has "angle","magnitude" as well as "addition","substraction","multiplication",etc. associated with it.By principle 2,"the square root of negative one"is correct for the blend but not the inputs.
Hence this was an example of category extension,and it doesn't merely involving adding or deleting features to input spaces,but a whole conceptual change is involved.

Source: #1
food for thought
Is blending the result of some deeper cognitive process or is the presented structure supposed to represent
the actual structure of cognition ?
How do we decide when, what spaces and in what ways to blend ?
REFERENCES
#1 Conceptual Integration Networks
Gilles Fauconnier and Mark Turner
COGNITIVE SCIENCE Vol22 (2) 1998, pp. 133-187
DOWNLOAD HERE
#2 Blending as a Central Process of Grammar
Gilles Fauconnier and Mark Turner
in Conceptual Structure, Discourse and Language, ed. Adele Goldberg. Cambridge University Press, 1996
DOWNLOAD HERE
#3 Polysemy and Conceptual Blending
Gilles Fauconnier and Mark Turner
in Polysemy: Flexible Patterns of Meaning in Mind and Language, 2003
DOWNLOAD HERE
